Elliptic Curve Cryptography (ECC) has existed since the mid-1980s, but it is still looked on as the newcomer in the world of SSL, and has only begun to gain adoption in the past few years. ECC is a fundamentally different mathematical approach to encryption than the venerable RSA algorithm. An elliptic curve is an algebraic function (y2 = x3 + ax + b) which looks like a symmetrical curve parallel to the x axis when plotted. (See figures below.) As with other forms of public key cryptography, ECC is based on a one-way property in which it is easy to perform a calculation but infeasible to reverse or invert the results of the calculation to find the original numbers. ECC uses different mathematical operations than RSA to achieve this property. The easiest way to explain this math is — for an elliptic curve, a line will only pass through three points along the curve (P, Q, and R), and that by knowing two of the points (P and Q), the other (R) can be calculated easily, but with just R, the other two, P and Q, cannot be derived.
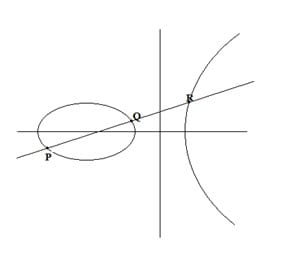
Elliptic Curve #1
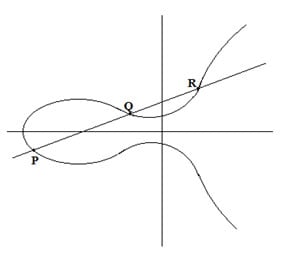
Elliptic Curve #2
ECC is used in both digital signatures via Elliptic Curve DSA (ECDSA), and in key exchange via Elliptic Curve Diffie-Hellman (ECDH). These algorithms are applied in different parts of the SSL standard. First, SSL certificates can be signed with ECDSA instead of RSA. The second use for ECC is during the handshake when the Web server and client are negotiating session keys that are used to encrypt all of the data sent between the server and browser. In this latter case, the server and browser must both be configured to support ECDH cipher suites as described in our post on server configuration. The US government has endorsed ECC by including it in the Suite B standard.
Benefits
The foremost benefit of ECC is that it’s simply stronger than RSA for key sizes in use today. The typical ECC key size of 256 bits is equivalent to a 3072-bit RSA key and 10,000 times stronger than a 2048-bit RSA key! To stay ahead of an attacker’s computing power, RSA keys must get longer. The CA/Browser Forum and leading browser vendors officially ended support for 1024-bit RSA keys after 2013, so all new SSL certificates must use keys that are twice as long. Moreover, as shown in the table below, future RSA key sizes quickly expand while ECC key lengths increase linearly with strength.
| Symmetric Key Size (bits) | RSA and DSA Key Size (bits) | ECC Key Size (bits) | |92 | 7680 | 384 | | 56 | 15360 | 512 |
Source: NIST 800-57, Table 2 (http://csrc.nist.gov/publications/nistpubs/800-57/sp800-57_part1_rev3_general.pdf)
Another security benefit of ECC is simply that it provides an alternative to RSA and DSA. If a major weakness in RSA is discovered, ECC is likely to be the best alternative, especially if the RSA weakness suddenly requires a sharp increase in key size to compensate.
ECC is also faster for a number of reasons. First off, smaller keys means less data that must be transmitted from the server to the client during an SSL handshake. In addition, ECC requires less processing power (CPU) and memory, resulting in significantly faster response times and throughput on Web servers when it is in use.
A third critical benefit of using ECC is Perfect Forward Secrecy (PFS). While PFS is not a property of ECC, the cipher suites supported by modern Web servers and browsers that implement PFS also implement ECC. Web servers that prefer Ephemeral ECDH (ECDHE) using cipher suites such as “TLS_ECDHE_RSA_WITH_AES_256_CBC_SHA” gain the benefits of both ECC and PFS.
Cautions
We recommend that you consider ECC to gain the benefits noted above, but there are a few things that should be considered. Probably the most important is that some browsers don’t support ECC certificates. Microsoft built support for ECC into Windows Vista, but earlier versions including Windows XP do not support ECC. Mozilla added ECC support in an early version of Firefox, and the current version of Apple’s OS X also supports ECC, as do the current versions of Chrome and Opera on all platforms.
Reliable information on ECC support in mobile platforms isn’t currently available. One solution to this problem is to use the Web server to deliver different certificates based on the client’s capabilities. For instance, Apache can be configured to negotiate ECC with clients that support it, and to negotiate RSA with the remainder of the clients
Another concern for websites that serve a significant number of mobile users is that – while testing has shown that ECC is faster overall – ECC signature verification is a compute intensive task and it can be slower than RSA on devices with slower processors. Unknown vulnerabilities pose another risk for ECC. Side-channel / timing attacks are theoretically possible, and since ECC support in many applications is newer, the discovery of vulnerabilities in specific implementations is not out of the question.
A final concern with ECC is that there are many patents in this area, creating some risk and uncertainty. Certicom Corp., a subsidiary of BlackBerry Ltd., holds over 350 patents that cover many aspects of ECC such as performance and security optimizations. However, many believe that Certicom only holds patents on specific implementations of ECC and in all cases there are alternatives that are not encumbered by patents. Our best advice is to ask your Certificate Authority if you have any concerns with ECC patents.
Conclusion
In summary, ECC is a fundamental improvement in the cryptography used in SSL. It provides a number of benefits including increased strength and performance. Moreover, it provides a viable alternative to the aging algorithms that so much of today’s systems rely on. We recommend that web servers be configured to prefer ECC cipher suites today, and while we expect RSA to be predominate in SSL certificates for some time, ECC is an alternative with a bright future.





























































































